Алгоритмы сортировки: зачем они нужны?
А зачем вообще нужны алгоритмы сортировки, если исключить собеседования? Как часто мы применяем их на практике, а если и применяем, то правильно ли? Давайте разбираться.
- Ложка теории
- Бочка практики
- Почему их так любят на собеседованиях?
- Где на практике применяются алгоритмы сортировки?
- Выводы
Ложка теории
Сортировка данных — одна из алгоритмических категорий, к которым программисту следует привыкнуть. В первую очередь, конечно же, вы столкнётесь с сортировкой на этапе обучения. Задачи, где что-то нужно упорядочить по определённому признаку, — распространённая история, которая повторяется и на собеседованиях.
Сегодня существуют десятки алгоритмов сортировки. Прям на 100% одного идеального варианта нет: разные алгоритмы оптимальны для разных наборов и типов данных. Вы наверняка слышали или даже работали с самыми популярными из них:
- Пузырьковая сортировка
- Сортировка перемешиванием
- Сортировка расчёской
- Сортировка вставками
- Сортировка выбором
- Быстрая сортировка
- Пирамидальная сортировка
Одни алгоритмы просты в реализации и хорошо подходят для разъяснения принципов сортировки, другие — для работы с большими массивами данных, третьи оптимизированы по числу процессорных циклов, скорости, etc.
Вот так, например, выглядят 15 Алгоритмов сортировки за 6 минут.
Примечание Рекомендую убавить громкость.
Бочка практики
Чтобы понять, зачем нужны алгоритмы сортировки, следует проанализировать хотя бы несколько из них. Рассмотрим наиболее популярные алгоритмы в коде и с кратким объяснением.
Сортировка пузырьком
Сортировка пузырьком — один из самых известных алгоритмов сортировки. Его суть в последовательном сравнении значений двух соседних элементов слева направо: если предыдущее больше последующего, они меняются местами. При сортировке элементов по убыванию, наоборот: в конец списка уходят элементы с наименьшим значением.
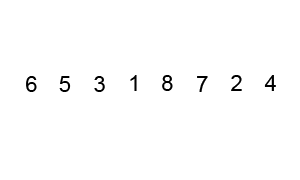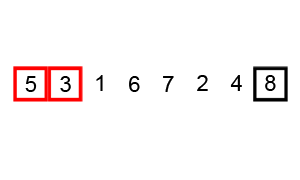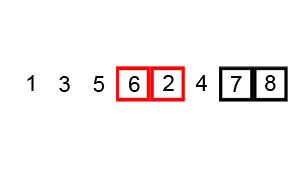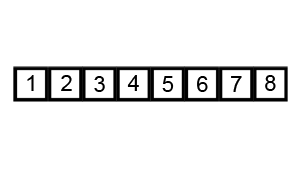
Код
public class BubbleSorter {
public static void sort(int[] array) {
//внешний цикл отвечает за номер прохода
for (int i = 0; i < array.length - 1; i++) {
//внутренний цикл -за перебор элементов в одном проходе
for (int j = array.length - 1; j > i; j--) {
if (array[j - 1] > array[j]) {
//переменная temp отвечает за обмен значений
int temp = array[j - 1];
array[j - 1] = array[j];
array[j] = temp;
}
}
}
}
}Здесь во внутреннем цикле перебираем значения, начиная с последнего (array.length - 1), и в каждом следующем проходе уменьшаем количество просмотренных элементов (j > i).
Сложность алгоритма: О(n2)
- Алгоритм хорошо себя показывает с большими наборами данных, где элементы почти отсортированы и требуется всего одна итерация, чтобы определить, отсортирован ли список до конца.
- В случае с совершенно неотсортированным списком, для пузырьковой сортировки он должен быть хотя бы небольшим.
Улучшенными версиями пузырькового метода являются сортировки перемешиванием (шейкерная) и расчёской.
Сортировка вставками
Это простая сортировка, при которой массив постепенно перебирается слева направо. При этом элемент сравнивается со всеми предыдущими элементами и размещается так, чтобы оказаться в подходящем месте среди ранее упорядоченных элементов. Так происходит до тех пор, пока набор входных данных не будет исчерпан.
Звучит сложно, но на деле это самый простой алгоритм сортировки.

Код
public class InsertionSort {
public static void sort(int[] array) {
int j;
//обходим список
for (int i = 1; i < array.length; i++) {
int temp = array[i];
for (j = i; j > 0 && temp < array[j - 1]; j--) {
array[j] = array[j - 1];
}
array[j] = temp;
}
}
}Сложность алгоритма: О(n2) для сравнений и перестановок.
- Как и в случае с пузырьковой сортировкой, этот алгоритм работает быстрее всего на очень маленьком или почти отсортированном наборе данных.
Этот алгоритм также используется как часть алгоритма сортировки Шелла.
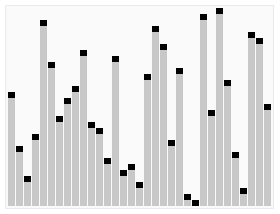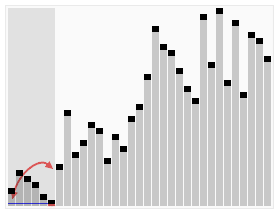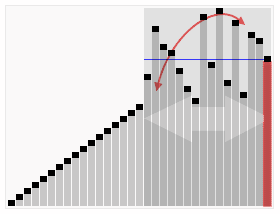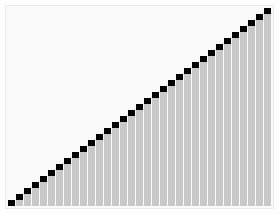
Быстрая сортировка
Быстрая сортировка относится к эффективным алгоритмам и состоит из нескольких шагов:
- Из массива выбирается опорный элемент, чаще всего посередине массива.
- Другие элементы массива распределяются таким образом, чтобы меньшие размещались до него, а большие — после.
- Далее первые шаги рекурсивно применяются к подмассивам, которые разделились опорным элементом на две части — слева и справа от него.
Код
public class QuickSort {
public static void sort(int[] array, int low, int high) {
//завершить,если массив пуст или уже нечего делить
if (array.length == 0 || low >= high) {
return;
}
//выбираем опорный элемент
int middle = low + (high - low) / 2;
int opora = array[middle];
//разделяем на подмассивы
int i = low, j = high;
while (i <= j) {
while (array[i] < opora) {
i++;
}
while (array[j] > opora) {
j--;
}
//меняем местами
if (i <= j) {
int temp = array[i];
array[i] = array[j];
array[j] = temp;
i++;
j--;
}
}
//рекурсия для сортировки левой и правой части
if (low < j) {
quickSort(array, low, j);
}
if (high > i){
quickSort(array, i, high);
}
}
}Сложность алгоритма: O(n log n)
- Быстрая сортировка считается самой быстрой, но она не всегда
O(n log n), так как в худших случаях она становитсяО(n2). - Быстрая сортировка более эффективна для наборов данных, которые помещаются в доступную память. Для больших наборов она неэффективна, и в этом случае более предпочтительна, например, сортировка слиянием.
- Быстрая сортировка — это сортировка на месте (т. е. она не требует дополнительной памяти), поэтому её целесообразно использовать для массивов.
Ещё больше алгоритмов сортировки с визуализацией и подробным объяснением.
Почему их так любят на собеседованиях?
Так работодатель преследует сразу несколько целей:
- Если вам дана возможность выбрать любой алгоритм сортировки на своё усмотрение, вас проверяют на понимание работы алгоритмов и грамотный подход к решению.
- Если вас просят реализовать конкретный алгоритм, делается упор на стиль написания кода.
- Иногда для задачи даётся намеренно неправильный алгоритм, например такой, с которым сортировка займёт больше времени или памяти. Тогда вам нужно озвучить и аргументировать более выгодный вариант. Это продемонстрирует ваше умение анализировать задачу и отстаивать своё мнение.
Очень важно понимать механизм работы того или иного алгоритма. Допустим, быстрая сортировка предпочтительнее для массивов, а сортировка слиянием — для связных списков. Дело в том, что в связном списке для доступа к данным по индексу нужно пройти от головы до этого индекса. Сортировка слиянием обращается к данным последовательно, и потребность в произвольном доступе невелика.
Если вы готовитесь к собеседованию, обязательно погоняйте себя на знание и, что немаловажно, понимание алгоритмов сортировки.
Где на практике применяются алгоритмы сортировки?
Кто бы что ни говорил, а на практике это тоже бывает полезно. Да, зачастую мы заочно сортируем данные, например через SQL-запрос с оператором ORDER BY. Или если у вас небольшой понятный массив, можно воспользоваться встроенной функцией языка типа sort() в JavaScript. Но не всегда условия просты в выполнении.
Сложности с сортировкой начинаются, когда:
- это работа с массивами данных на десятки или сотни тысяч элементов;
- затруднён доступ к этим данным;
- нужно оптимизировать время выполнения или требуемый объём памяти.
К примеру, в Salesforce-разработке мне приходилось не раз сталкиваться с условиями, в которых без сортировки не обойтись. Это актуально, когда нужен не просто запрос к базе данных, а соответствие искомого элемента нескольким условиям + запуск дополнительных процессов между проверками соответствия этим условиям. При этом проекты были большими, и каждый процесс тщательно оптимизировался, дабы сэкономить время и память.
Для веба это нормальная история. Игры, такие как знаменитая головоломка французского математика Эдуарда Люка «Ханойская башня», тоже потребуют от вас понимания сортировки. Ряд математических решений и работа со строками порой не обходятся без упорядочивания данных. Есть уйма примеров, но суть одна: алгоритмы сортировки — это далеко не всегда только про собеседования.
Выводы
Так зачем же нужны алгоритмы сортировки на практике?
- Чтобы иметь чёткое представление, как работает алгоритм и как он ляжет на синтаксис конкретного языка программирования.
- Чтобы тренировать алгоритмическое мышление.
- Чтобы уметь реализовывать алгоритмы там, где нет подходящей готовой библиотеки.

